前言

部分内容摘自程杰的《大话数据结构》

1. 希尔排序

给大家出一道智力题。请问 “VII” 是什么?
嗯，很好，它是罗马数字的 7。现在我们要给它加上一笔，让它变成 8（VIII），应该是非常简单，只需要在右侧加一-竖线即可。
现在我请大家试着对罗马数字 9，也就是“IX" 增加一笔，把它变成6,应该怎么
做?
我这里有 3 种另类的方法可以实现它。
方法一：观察发现 “X” 其实可以看作是一个正放一个倒置两个 “V”。因此我们，给 “IX” 中间加一条水平线，上下颠倒，然后遮住下面部分，也就是说，我们所谓的加上一笔就是遮住一部分，于是就得到 “VI”，如下图所示。

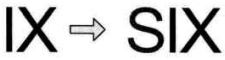
方法二：在 “IX” 前面加一个 “S”，此时构成一个英文单词 “SIX”，这就等于得到一个 6 了。哈哈，我听到下面一片哗然，我刚有没有说一定要是 “VI” 呀，我只说把它变成 6 而已，至于是罗马数字还是英文单词，我可没有限制。显然，你们的思维受到了我前面举例的 “VII” 转变为 “VII” 的影响，如下图所示。

方法三：在 “IX” 后面加一个 “6”，得到 “1X6”，其结果当然是数字 6 了。大家笑了，因为这个想法实在是过分，把字母 “I” 当成了数字 1，字母 “X” 看成了乘号。可谁又规定说这是不可以的呢？只要没违反规则，得到 6 即可，如下图所示。

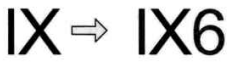
智力题的答案介绍完了。大家会发现，看似解决不了的问题，还真不一定就没有办法，也许只是暂时没想到罢了。
我们都能理解，优秀排序算法的首要条件就是速度。于是人们想了许许多多的办法，目的就是为了提高排序的速度。而在很长的时间里，众人发现尽管各种排序算法花样繁多（比如前面我们提到的三种不同的排序算法），但时间复杂度都是 $O(n^2)$ ，似乎没法超越了。此时，计算机学术界充斥着 “排序算法不可能突破 $O(n^2)$ ” 的声音。就像刚才大家做智力题的感觉-一样，“不可能” 成了主流。
终于有一天，当一位科学家发布超越了 $O(n^2)$ 新排序算法后，紧接着就出现了好几种可以超越 $O(n^2)$ 的排序算法，并把内排序算法的时间复杂度提升到了 $O(nlogn)$ 。 “不可能超越 $O(n^2)$ ” 彻底成为了历史。
从这里也告诉我们，做任何事，你解决不了时，想一想 “Nothing is impossible!"，虽然有点唯心，但这样的思维方式会让你更加深入地思考解决方案，而不是匆忙的放弃。

1.1 希尔排序原理

现在，我要讲解的算法叫希尔排序（Shell Sort）。希尔排序是 D.L.Shell 于 1959 年提出来的一种排序算法，在这之前排序算法的时间复杂度基本都是 $O(nlogn)$ 的，希尔排序算法是突破这个时间复杂度的第一批算法之一。
我们上篇讲的直接插入排序，应该说，它的效率在某些时候是很高的，比如，我们的记录本身就是基本有序的，我们只需要少量的插入操作，就可以完成整个记录集的排序工作，此时直接插入很高效。还有就是记录数比较少时，直接插入的优势也比较明显。可问题在于，两个条件本身就过于苛刻，现实中记录少或者基本有序都属于特殊情况。
不过别急，有条件当然是好，条件不存在，我们创造条件也是可以去做的。于是科学家希尔研究出了一种排序方法，对直接插入排序改进后可以增加效率。
如何让待排序的记录个数较少呢？很容易想到的就是将原本有大量记录数的记录进行分组。分割成若千个子序列，此时每个子序列待排序的记录个数就比较少了，然后在这些子序列内分别进行直接插入排序，当整个序列都基本有序时，注意只是基本有序时，再对全体记录进行一次直接插入排序。
此时一定有人开始疑惑了。这不对呀，比如我们现在有序列是 {9,1,5,8,3,7,4,6,2}，现在将它分成三组，{9,1,5}， {8,3,7}，{4,6,2}，哪怕将它们各自排序排好了，变成 {1,5,9}，{3,7,8}，{2,4,6}，再合并它们成 {1,5,9,3,7,8,2,4,6}，此时,这个序列还是杂乱无序，谈不上基本有序，要排序还是重来一遍直接插入有序，这样做有用吗？需要强调一下，所谓的基本有序，就是小的关键字基本在前面，大的基本在后面，不大不小的基本在中间，像 {2,1,3,6,4,7,5,8,9} 这样可以称为基本有序了。但像 {1,5,9,3,7,8,2,4,6} 这样的 9 在第三位，2 在倒数第三位就谈不上基本有序。
问题其实也就在这里，我们分割待排序记录的目的是减少待排序记录的个数，并使整个序列向基本有序发展。而如上面这样分完组后就各自排序的方法达不到我们的要求。因此，我们需要采取跳跃分割的策略：将相距某个 “增量” 的记录组成一个子序列，这样才能保证在子序列内分别进行直接插入排序后得到的结果是基本有序而不是局部有序。

1.2 希尔排序算法

希尔排序算法代码如下。

/* 对顺序表L作希尔排序 */
void ShellSort(SqList *L)
{
	int i,j;
	int increment=L->length;
	do
	{
		increment=increment/3+1;	/* 增量序列 */
		for(i=increment+1;i<=L->length;i++)
		{
			if (L->r[i]<L->r[i-increment])
			{/* 需将L->r[i]插入有序增量子表 */
				L->r[0]=L->r[1];	/* 暂存在L->r[0] */
				for (j=i-increment;j>0&&L->r[0]<L->r[j];j-=increment)
					L->r[j+increment]=L->r[j];	/* 记录后移，查找插入位置 */
				L->r[j+increment]=L->r[0];	/* 插入 */
			}
		}
	}
	while (increment>1);
}

程序开始运行，此时我们传入的SqList参数的值为length=9，r[10]={0,9,1,5,8,3,7,4,6,2}。这就是我们需要等待排序的序列，如下图所示。
第 4 行，变量increment就是那个 “增量”，我们初始值让它等于待排序的记录数。
第 5~19 行是一个do循环，它提终止条件是increment不大于 1 时，其实也就是增量为 1 时就停止循环了。
第 7 行，这一句很关键，但也是难以理解的地方，我们后面还要谈到它，先放一放。这里执行完成后，increment=9/3+1=4。
第 8~17 行是一个for循环，i从4+1=5开始到 9 结束。
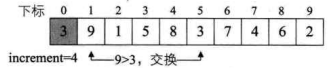
第 10 行，判断L.r[i]与L.r[i-increment]大小，L.r[5]=3小于L.r[i-increment]=L.r[1]=9，满足条件，第 12 行，将L.r[5]=3暂存入L.r[0]。第 13~14 行的循环只是为了将L.r[1]=9的值赋给L.r[5]，由于循环的增量是j-=increment<其实它就循环了一次，此时j=-3。第 15 行，再将L.r[0]=3赋值给L.r[j+increment]=L.r[-3+4]=L.r[1]=3。如下图所示，事实上，这一段代码就干了一件事，就是将第 5 位的 3 和第 1 位的 9 交换了位置。
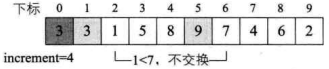
循环继续，i=6，L.r[6]=7>L.r[i-increment]=L.r[2]=1，因此不交换两者数据。如下图所示。
循环继续，i=7，L.r[7]=4<L.r[i-increment]=L.r[3]=5，交换两者数据。如下图所示。
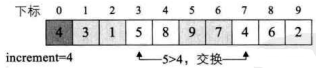
循环继续，i=8，L.r[8]=6<L.r[i-increment]=L.r[4]=8，交换两者数据。如下图所示。
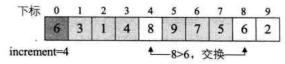
循环继续，i=9，L.r[9]=2<L.r[i-increment]=L.r[5]=9，交换两者数据。注意，第 13~14 行是循环，此时还要继续比较L.r[5]与L.r[1]的大小，因为2<3，所以还要交换L.r[5]与L.r[1]的数据，如下图所示。

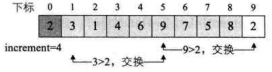
最终第一轮循环后，数组的排序结果为下图所示。细心的人会发现，我们的数字 1、2 等小数字已经在前两位，而 8、9 等大数字已经在后两位，也就是说，通过这样的排序，我们已经让整个序列基本有序了。这其实就是希尔排序的精华所在，它将关键字较小的记录，不是一步一步地往前挪动，而是跳跃式地往前移，从而使得每次完成一轮循环后，整个序列就朝着有序坚实地迈进一步。
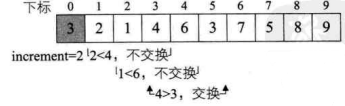
我们继续，在完成一轮do循环后，此时由于increment=4>1因此我们需要继续do循环。第 7 行得到increment=4/3+1=2，第 8~17 行for循环，i从2+1=3开始到 9 结束。当i=3、4时，不用交换，当i=5时，需要交换数据，如下图所示。
此后，i=6、7、8、9均不用交换，如下图所示。
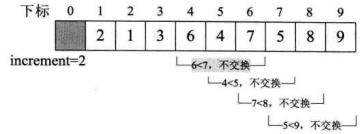
再次完成一轮do循环，increment=2>1，再次do循环，第 7 行得到increment=2/3+1=1，此时这就是最后一轮do循环了。尽管第 8~17 行for循环，i从1+1=2开始到 9 结束，但由于当前序列已经基本有序，可交换数据的情况大为减少，效率其实很高。如下图所示，图中箭头连线为需要交换的关键字。

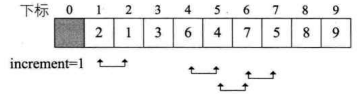
最终完成排序过程，如下图所示。

1.3 希尔排序复杂度分析

通过这段代码的剖析，相信大家有些明白，希尔排序的关键并不是随便分组后各自排序，而是将相隔某个 “增量” 的记录组成一个子序列，实现跳跃式的移动，使得排序的效率提高。
这里“增量"的选取就非常关键了。我们在代码中第 7 行，是用increment=increment/3+1;的方式选取增量的，可究竟应该选取什么样的增量才是最好，目前还是一个数学难题，迄今为止还没有人找到一种最好的增量序列。不过大量的研究表明，当增量序列为 $dlta[k]=2^{t-k+1}-1(0\leq k\leq t\leq\lfloor log_2(n+1)\rfloor)$ 时，可以获得不错的效率，其时间复杂度为 $O(n^{3/2})$ ，要好于直接排序的 $O(n^2)$ 。需要注意的是，增量序列的最后一个增量值必须等于1才行。另外由于记录是跳跃式的移动，希尔排序并不是一种稳定的排序算法。
不管怎么说，希尔排序算法的发明，使得我们终于突破了慢速排序的时代（超越了时间复杂度为 $O(n^2)$ ），之后，相应的更为高效的排序算法也就相继出现了。