《数据结构与算法》(十八)- 平衡二叉树
前言
部分内容摘自程杰的《大话数据结构》
1. 平衡二叉树(AVL树)
有一部德国人制作的叫《平衡》(英文名:Balance)的短片,它在 1989 年获得奥斯卡最佳短片奖。说的是在空中,悬浮着一个四方的平板,上面站立着 5 个人,同样的相貌,同样的装束,同样的面无表情。平板的中心是个看不见的支点,为了平衡,5 个人必须寻找合适的位置。原本,简单的站在中心就可以了,可是,如同我们一样,他们也好奇于这个世界,想知道下面是什么样子。而随着一个箱子的来临,这种平衡被打破了,箱子带来了音乐,带来了兴奋,也带来了不平衡,带来了分歧和斗争。
平板就是一个世界,当诱惑降临,当人心中的平衡被打破,世界就会混乱,最后留下的只有孤独寂寞失败。这种单调的机械化社会,禁不住诱惑的侵蚀,很容易崩溃。最容易被侵蚀的,恰恰是最空虚的心灵。
平衡二叉树(Self-Balancing Binary Search Tree 或 HejghtBalanced Binary Search Tree),是一种二叉排序树,其中每一个节点的左子树和右子树的高度差至多等于1。
有两位俄罗斯数学家 GM.Adeson-Velskii 和 E.M.Landis 在 1962 年共同发明一种解决平衡二叉树的算法,所以有不少资料中也称这样的平衡二叉树为AVL树。
从平衡二叉树的英文名字,你也可以体会到,它是一种高度平衡的二叉排序树。那什么叫做高度平衡呢?意思是说,要么它是一棵空树,要么它的左子树和右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值不超过 1。我们将二叉树上结点的左子树深度减去右子树深度的值称为平衡因子BF(Balance Factor),那么平衡二叉树上所有结点的平衡因子只可能是-1、0和1。只要二叉树上有一个结点的平衡因子的绝对值大于 1,则该二叉树就是不平衡的。
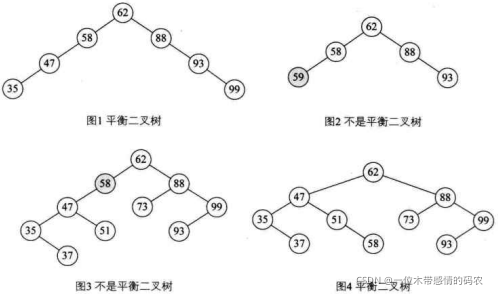
看下图,为什么图 1 是平衡二叉树,而图 2 却不是呢?这里就是考查我们对平衡二叉树的定义的理解,它的前提首先是一棵二叉排序树,图 2 的 59 比 58 大,却是 58 的左子树,这是不符合二叉排序树的定义的。图 3 不是平衡二叉树的原因就在于,结点 58 的左子树高度为 2,而右子树为空,二者差大于了绝对值 1,因此它也不是平衡的。而经过适当的调整后的图 4,它就符合了定义,因此它是平衡二叉树。
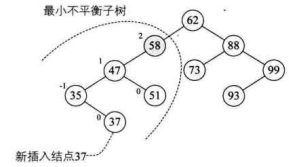
距离插入结点最近的,且平衡因子的绝对值大于1的结点为根的子树,我们称为最小不平衡子树。下图中,当新插入结点 37 时,距离它最近的平衡因子绝对值超过 1 的结点是 58(即它的左子树高度 2 减去右子树高度 0),所以从 58 开始以下的子树为最小不平衡子树。
1.1 平衡二叉树实现原理
平衡二叉树构建的基本思想就是在构建二叉排序树的过程中,每当插入一个结点时,先检查是否因插入而破坏了树的平衡性,若是,则找出最小不平衡子树。在保持二叉排序树特性的前提下,调整最小不平衡子树中各结点之间的链接关系,进行相应的旋转,使之成为新的平衡子树。
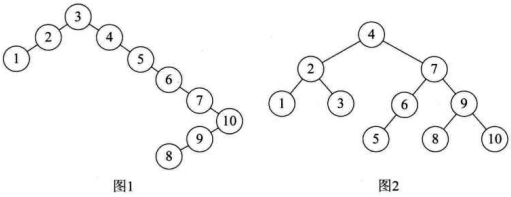
为了能在讲解算法时轻松一些, 我们先讲一个平衡二叉树构建过程的例子。假设我们现在有一个数组a[10]={3,2,1,4,5,6,7,10,9,8}需要构建二叉排序树。在没有学习平衡二叉树之前,根据二叉排序树的特性,我们通常会将它构建成如下图的图 1 所示的样子。虽然它完全符合二叉排序树的定义,但是对这样高度达到 8 的二叉树来说,查找是非常不利的。我们更期望能构建成如下图的图2的样子,高度为 4 的二叉排序树才可以提供高效的查找效率。那么现在我们就来研究如何将一个数组构建出图 2 的树结构。
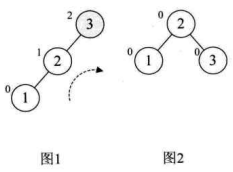
对于数组a[10]={3,2,1,4,5,6,7,10,9,8}的前两位 3 和 2,我们很正常地构建,到了第 3 个数 “1” 时,发现此时根结点 “3” 的平衡因子变成了 2,此时整棵树都成了最小不平衡子树,因此需要调整,如下图的图 1(结点左上角数字为平衡因子BF值)。因为BF值为正,因此我们将整个树进行右旋(顺时针旋转),此时结点 2 成了根结点,3 成了 2 的右孩子,这样三个结点的BF值均为 0,非常的平衡,如下图的图 2 所示。
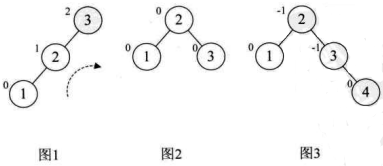
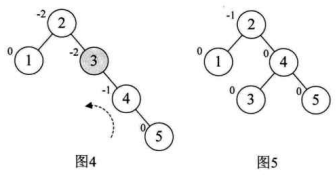
然后我们再增加结点 4,平衡因子没发生改变,如图 3。增加结点 5 时,结点 3 的BF值为 -2,说明要旋转了。由于BF是负值,所以我们对这棵最小平衡子树进行左旋(逆时针旋转),如图 4,此时我们整个树又达到了平衡。
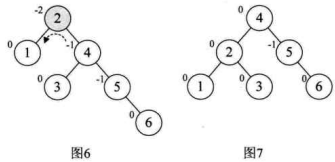
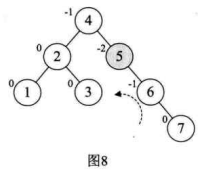
继续,增加结点 6 时,发现根结点 2 的BF值变成了 -2,如下图的图 6。所以我们对根结点进行了左旋,注意此时本来结点 3 是 4 的左孩子,由于旋转后需要满足二叉排序树特性,因此它成了结点 2 的右孩子,如图 7。增加结点 7,同样的左旋转,使得整棵树达到平衡,如图 8 和图 9 所示。
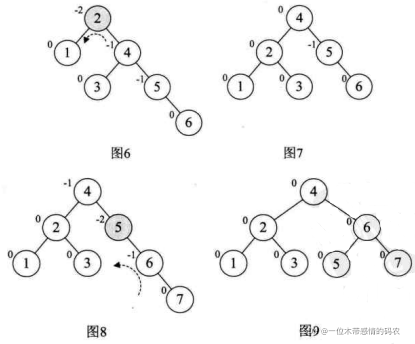
当增加结点 10 时,结构无变化,如下图的图 10。再增加结点 9,此时结点 7 的BF变成了 -2,理论上我们只需要旋转最小不平衡子树 7、9、 10 即可,但是如果左旋转后,结点 9 就成了 10 的右孩子,这是不符合二叉排序树的特性的,此时不能简单的左旋,如图 11 所示。
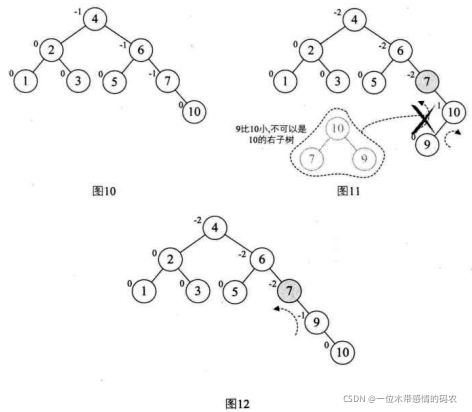
仔细观察图 11,发现根本原因在于结点 7 的BF是 -2,而结点 10 的BF是 1,也就是说,它们俩一正一负, 符号并不统一, 而前面的几次旋转,无论左还是右旋,最小不平衡子树的根结点与它的子结点符号都是相同的。这就是不能直接旋转的关键。那怎么办呢?
不统一,不统一就把它们先转到符号统一再说, 于是我们先对结点 9 和结点 10 进行右旋,使得结点 10 成了 9 的右子树,结点 9 的BF为 -1,此时就与结点 7 的BF值符号统一了, 如上图的图 12 所示。
这样我们再以结点 7 为最小不平衡子树进行左旋,得到下图的图 13。接着插入 8,情况与刚才类似,结点 6 的BF是 -2,而它的右孩子 9 的BF是 1,如图 14,因此首先以 9 为根结点,进行右旋,得到图 15,此时结点 6 和结点 7 的符号都是负,再以 6 为根结点左旋,最终得到最后的平衡二叉树,如下图的图 16 所示。
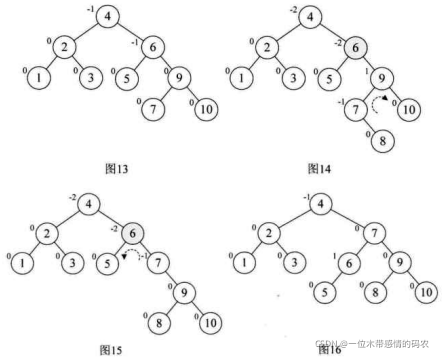
西方有一句民谣是这样说的:“丢失一个钉子,坏了一只蹄铁;坏了一只蹄铁,折了一匹战马;折了一匹战马,伤了一位骑士;伤了一位骑士,输了一场战斗;输了一场战斗,亡了一个帝国。”相信大家应该有点明白,所谓的平衡二叉树,其实就是在二叉排序树创建过程中保证它的平衡性,一旦发现有不平衡的情况,马上处理,这样就不会造成不可收拾的情况出现。通过刚才这个例子,你会发现,当最小不平衡子树根结点的平衡因子BF是大于 1 时,就右旋,小于 -1 时就左旋,如上例中结点 1、5、6、7 的插入等。插入结点后,最小不平衡子树的BF与它的子树的BF符号相反时,就需要对结点先进行一次旋转以使得符号相同后,再反向旋转一次才能够完成平衡操作,如上例中结点 9、8 的插入时。
1.2 平衡二叉树实现算法
好了,有这么多的准备工作,我们可以来讲解代码了。首先是需要改进二叉排序树的结点结构,增加一个BF,用来存储平衡因子。
1 | /* 二叉树的二叉链表结点结构定义 */ |
然后,对于右旋操作,我们的代码如下。
1 | /* 对以p为根的二又排序树作右旋处理, */ |
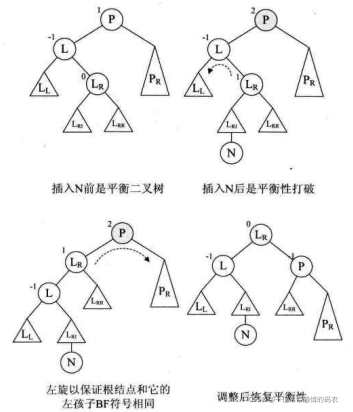
此函数代码的意思是说,当传入一个二叉排序树P,将它的左孩子结点定义为L,将L的右子树变成P的左子树,再将P改成L的右子树,最后将L替换P成为根结点。这样就完成了一次右旋操作,如下图所示。图中三角形代表子树,N代表新增结点。
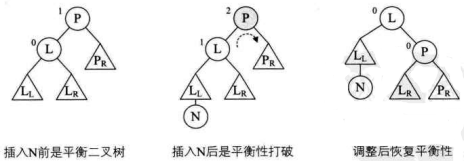
上面例子中的新增加结点N(如下图的图 1 和图 2),就是右旋操作。
左旋操作代码如下。
1 | /* 对以p为根的二又排序树作左旋处理, */ |
这段代码与右旋代码是对称的,在此不做解释了。上面例子中的新增结点 5、6、7(具体见下图),都是左旋操作。
现在我们来看左平衡旋转处理的函数代码。
1 |
|
首先,我们定义了三个常数变量,分别代表 1、0、-1。
- 函数被调用,传入一个需调整平衡性的子树
T。由于LeftBalance()函数被调用时,其实是已经确认当前子树是不平衡状态,且左子树的高度大于右子树的高度。换句话说,此时T的根结点应该是平衡因子BF的值大于 1 的数。 - 第 4 行,我们将
T的左孩子赋值给L。 - 第 5~27 行是分支判断。
- 当
L的平衡因子为LH,即为 1 时,表明它与根结点的BF值符号相同,因此,第 8 行,将它们的BF值都改为 0,并且第 9 行,进行右旋操作。操作的方式如本节的图 1 、图 2 所示。 - 当
L的平衡因子为RH,即为 -1 时,表明它与根结点的BF值符号相反,此时需要做双旋处理。第 13~22 行,针对L的右孩子 L 的BF作判断,修改根结点T和L的BF值。第 24 行将当前 L 的BF改为 0。 - 第 25 行,对根结点的左子树进行左旋,如下图第二图所示。
- 第 26 行,对根结点进行右旋,如下图的第三图所示,完成平衡操作。
同样的,右平衡旋转处理的函数代码非常类似,直接看代码,不做讲解了。
我们前面例子中的新增结点 9 和 8 就是典型的右平衡旋转,并且双旋完成平衡的例子(此前的图 11、图 14 就是类似样例)。
有了这些准备,我们的主函数才算是正式登场了。
1 | /* 若在平衡的二叉排序树下中不存在和e有相同关键字的结点,则插入一个 */ |
- 程序开始执行时,第 3~10 行是指当前
T为空时,则申请内存新增一个结点。 - 第 13~17 行表示当存在相同结点,则不需要插入。
- 第 18~40 行,当新结点
e小于T的根结点值时,则在T的左子树查找。 - 第 20~21 行,递归调用本函数,直到找到则返回
fase,否则说明插入结点成功,执行下面语句。 - 第 22~39 行,当
taller为TRUE时,说明插入了结点,此时需要判断T的平衡因子,如果是 1,说明左子树高于右子树,需要调用LeftBalance函数进行左平衡旋转处理。如果为 0 或 -1,则说明新插入结点没有让整棵二叉排序树失去平衡性,只需要修改相关的BF值即可。 - 第 41~63 行,说明新结点
e大于T的根结点的值,在T的右子树查找。代码上述类似,不再详述。
对于这段代码来说,我们只需要在需要构建平衡二叉树的时候执行如下列代码即可在内存中生成一棵与下图相同的平衡的二叉树。
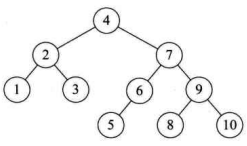
1 | int i; |
如果我们需要查找的集合本身没有顺序,在频繁查找的同时也需要经常的插入和删除操作,显然我们需要构建一棵二叉排序树, 但是不平衡的二叉排序树,查找效率是非常低的,因此我们需要在构建时,就让这棵二叉排序树是平衡二叉树,此时我们的查找时间复杂度就为 ,而插入和删除也为 。 这显然是比较理想的一种动态查找表算法。
2. 总结
二叉排序树是动态查找最重要的数据结构,它可以在兼顾查找性能的基础上,让插入和删除也变得效率较高。不过为了达到最优的状态,二叉排序树最好是构成平衡的二叉树才是最佳。了解AVL树是如何处理平衡性的问题,是重中之重。




