前言

部分内容摘自程杰的《大话数据结构》

1. 二叉排序树

大家可能都听过这个故事，说有两个年轻人正在深山中行走。忽然发现远处有一只老虎要冲过来，怎么办？其中一个赶忙弯腰系鞋带，另一个奇怪地问：“你系鞋带干什么？你不可能跑得比老虎还快。” 系鞋带者说：“我有什么必要跑赢老虎呢？我只要跑得比你快就行了。”
这真是交友不慎呀！别急，如果你的朋友是系鞋带者，你怎么办？
后来老虎来了，系鞋带者拼命地跑，另一人则急中生智，爬到了树上。老虎在选择爬树还是追人之间，当然是会选择后者，于是结果······爬树者改变了跑的思想，这一改变何等重要，捡回了自己的一条命。
假设查找的数据集是普通的顺序存储，那么插入操作就是将记录放在表的末端，给表记录数加一即可，删除操作可以是删除后，后面的记录向前移，也可以是要删除的元素与最后一个元素互换，表记录数减一，反正整个数据集也没有什么顺序，这样的效率也不错。应该说，插入和删除对于顺序存储结构来说，效率是可以接受的，但这样的表由于无序造成查找的效率很低，前面我们有讲解，这就不在哆嗦。
如果查找的数据集是有序线性表，并且是顺序存储的，查找可以用折半、插值、斐波那契等查找算法来实现，可惜，因为有序，在插入和删除操作上，就需要耗费大量的时间。
有没有一种即可以使得插入和删除效率不错，又可以比较高效率地实现查找的算法呢？还真有。
我们在前面把这种需要在查找时插入或删除的查找表称为动态查找表。我们现在就来看看什么样的结构可以实现动态查找表的高效率。
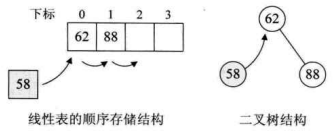
如果在复杂的问题面前，我们束手无策的话，不妨先从最最简单的情况入手。现在我们的目标是插入和查找同样高效。假设我们的数据集开始只有一个数 {62}，然后现在需要将 88 插入数据集，于是数据集成了 {62,88}，还保持着从小到大有序。再查找有没有 58，没有则插入，可此时要想在线性表的顺序存储中有序，就得移动 62 和 88 的位置，如左下图，可不可以不移动呢？嗯，当然是可以，那就是二叉树结构。当我们用二叉树的方式时，首先我们将第一个数 62 定为根结点，88 因为比 62 大，因此让它做 62 的右子树，58 因比 62 小，所以成为它的左子树。此时 58 的插入并没有影响到 62 与 88 的关系，如右下图所示。

也就是说，若我们现在需要对集合 {62,88,58,47,35,73,51,99,37,93} 做查找，在我们打算创建此集合时就考虑用二又树结构，而且是排好序的二叉树来创建。如下图所示，62、88、58 创建好后，下一个数 47 因比 58 小，是它的左子树（见③），35 是 47 的左子树（见④），73 比 62 大，但却比 88 小，是 88 的左子树（见⑤），51 比 62 小。比 58 小。比 47 大，是 47 的右子树（见⑥），99 比 62、88 都大，是 88 的右子树（见⑦），37 比 62、58、47 都小，但却比 35 大，是 35 的右子树（见⑧），93 则因比 62、88 大是 99 的左子树（见⑨）。

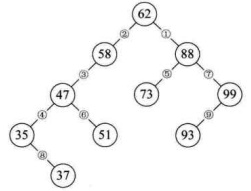
这样我们就得到了一棵二叉树，并且当我们对它进行中序遍历时，就可以得到一个有序的序列 {35,37,47,51,58,62,73,88,93,99}，所以我们通常称它为二叉排序树。
二叉排序树（Binary Sort Tree），又称为二叉查找树。它或者是一棵空树，或者是具有下列性质的二叉树。

若它的左子树不空，则左子树上所有结点的值均小于它的根结构的值；
若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
它的左、右子树也分别为二叉排序树。

从二叉排序树的定义也可以知道，它前提是二叉树，然后它采用了递归的定义方法，再者，它的结点间满足一定的次序关系，左子树结点一定比其双亲结点小，右子树结点一定比其双亲结点大。
构造一棵二叉排序树的目的，其实并不是为了排序，而是为了提高查找和插入删除关键字的速度。不管怎么说，在一个有序数据集上的查找，速度总是要快于无序的数据集的，而二叉排序树这种非线性的结构，也有利于插入和删除的实现。

1.1 二叉排序树的查找操作

首先我们提供一个二叉树的结构。

/* 二叉树的二叉链表结点结构定义 */
typedef" struct BiTNode	/* 结点结构 */
{
	int data;	/* 结点数据 */
	struct BiTNode *lchild, *rchild;	/* 左右孩子指针 */
} BiTNode, *BiTree;

然后我们来看看二叉排序树的查找是如何实现的。

/* 递归查找二叉排序树T中是否存在key, */
/* 指针f指向T的双亲，其初始调用值为NULL */
/* 若查找成功，则指针p指向该数据元素结点，并返回TRUE */
/* 否则指针p指向查找路径上访问的最后一个结点并返回FALSE */
Status SearchBST(BITree T, int key, BiTree f, BiTree *p)
{
	if (!T)	/* 查找不成功 */
	{
		p=f;
		return FALSE;
	}
	else if (key=T->data)	/* 查找成功 */
	{
		*p=T;
		return TRUE;
	}
	else if (key<T->data)
		return SearchBST(T->lchild, key, T, p);	/* 在左子树继续查找 */
	else
		return SearchBST(T->rchi1d, key, T, p);	/* 在右子树继续查找 */

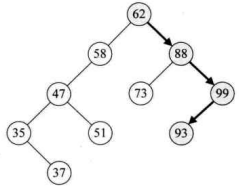
SearchBST()函数是一个可递归运行的函数，函数调用时的语句为SearchBST(T,93,NULL,p)，参数T是一个二叉链表，其中数据如下图所示，key代表要查找的关键字，目前我们打算查找 93，二叉树f指向T的双亲，当T指向根结点时，f的初值就为NULL，它在递归时有用，最后的参数p是为了查找成功后可以得到查找到的结点位置。
第 3~7 行，是用来判断当前二叉树是否到叶子结点，显然下图告诉我们当
前T指向根结点 62 的位置，T不为空，第 5~6 行不执行。
第 8~12 行是查找到相匹配的关键字时执行语句，显然93≠62，第 10~11 行不执行。
第 13~14 行是当要查找关键字小于当前结点值时执行语句，由于93>62，第 14 行不执行。
第 15~16 行是当要查找关键字大于当前结点值时执行语句，由于93>62，所以递归调用SearchBST(T->rchid, key, T, p)。此时T指向了 62 的右孩子 88，如下图所示。
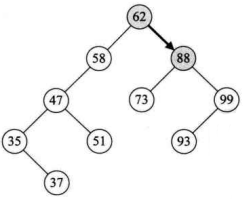
此时第二层SearchBST，因 93 比 88 大，所以执行第 16 行，再次递归调用SearchBST(T->rchildl, key, T, p)。此时T指向了 88 的右孩子 99，如下图所示。
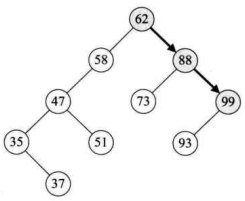
第三层的SearchBST，因 93 比 99 小，所以执行第 14 行，递归调用SearchBST(T->lchild, key, T, p)。此时T指向了 99 的左孩子 93，如下图所示。
第四层SearchBST，因key等于T->data，所以执行第 10~11 行，此时指针p指向 93 所在的结点，并返回True到第三层、第二层、第一层，最终函数返回True。

1.2 二叉排序树的插入操作

有了二叉排序树的查找函数，那么所谓的二叉排序树的插入，其实也就是将关键字放到树中的合适位置而已，来看代码。

/* 当二叉排序树T中不存在关键字等于key的数据元素时， */
/* 插入key并返回TRUE,否则返回FALSE */
Status InsertBSTt(BiTree *T，int key)
{
	BiTree p,s;
	if (!SearchBST(*T, key, NULL, p))	/* 查找不成功 */
	{
		s = (BiTree)malloc(sizeof(BiTNode));
		s->data=key;
		s->lchild = s->rchild = NULL;
		if (!p)
			*T=S;	/* 插入s为新的根结点 */
		else if(key<p->data )
			p->lchild=s;	/* 插入s为左孩子 */
		else
			p->rchild=s;	/* 插入s为右孩子 */
		return TRUE;
	}
	else
		return FALSE;	/* 树中已有关键字相同的结点，不再插入 */
}

这段代码非常简单。如果你调用函数是 “InsertBST(&T,93) ;"，那么结果就是FALSE，如果是 “InsertBST(&T,95);”，那么一定就是在 93 的结点增加一个右孩子 95，并且返回True。如下图所示。

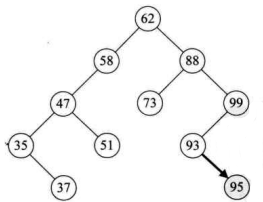
有了二叉排序树的插入代码，我们要实现二叉排序树的构建就非常容易了。下面的代码就可以创建一棵下图这样的树。

int i;
int a[10]={62,88,58,47,35,73,51,99,37,93};
BiTree T=NULL;
for (i=0;i<10;i++)
{
	InsertBST (&T，a[i]);
}

在你的大脑里，是否已经有一幅随着循环语句的运行逐步生成这棵二叉排序树的动画图案呢？如果不能，那只能说明你还没真理解它的原理哦。

1.3 二叉排序树删除操作

俗话说 “请神容易送神难”，我们已经介绍了二叉排序树的查找与插入算法，但是对于二叉排序树的删除，就不是那么容易，我们不能因为删除了结点，而让这棵树变得不满足二叉排序树的特性，所以删除需要考虑多种情况。
如果需要查找并删除如 37、 51、 73、93 这些在二叉排序树中是叶子的结点，那是很容易的，毕竞删除它们对整棵树来说，其他结点的结构并未受到影响，如下图所示。

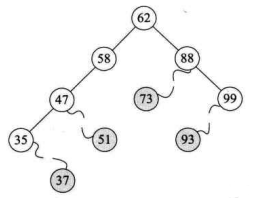
对于要删除的结点只有左子树或只有右子树的情况，相对也比较好解决。那就是结点删除后，将它的左子树或右子树整个移动到删除结点的位置即可，可以理解为独子继承父业。比如下图，就是先删除 35 和 99 结点，再删除 58 结点的变化图，最终，整个结构还是一个二叉排序树。

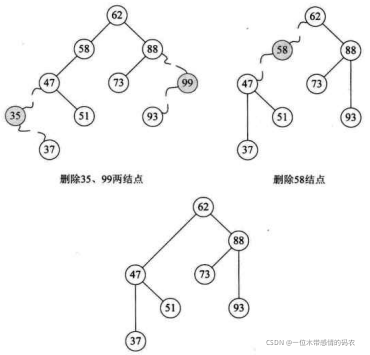
但是对于要删除的结点既有左子树又有右子树的情况怎么办呢？比如下图中的 47 结点若要删除了，它的两儿子以及子孙们怎么办呢？

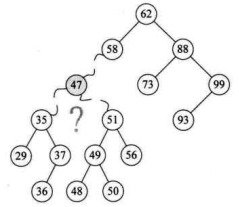
起初的想法，我们当 47 结点只有一个左子树，那么做法和一个左子树的操作一样，让 35 及它之下的结点成为 58 的左子树，然后再对 47 的右子树所有结点进行插入操作，如下图所示。这是比较简单的想法，可是 47 的右子树有子孙共 5 个结点，这么做效率不高且不说，还会导致整个二叉排序树结构发生很大的变化，有可能会增加树的高度。增加高度可不是个好事，这我们待会再说，总之这个想法不太好。

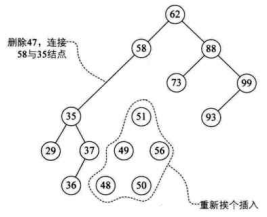
我们仔细观察一下，47 的两个子树中能否找出一个结点可以代替 47 呢？果然有，37 或者 48 都可以代替 47，此时在删除 47 后，整个二叉排序树并没有发生什么本质的改变。
为什么是 37 和 48？对的，它们正好是二叉排序树中比它小或比它大的最接近 47 的两个数。也就是说，如果我们对这棵二叉排序树进行中序遍历，得到的序列 {29,35,36,37,47,48,49,50,51,56,58,62,73,88,93,99}，它们正好是 47 的前驱和后继。
因此，比较好的办法就是，找到需要删除的结点p的直接前驱（或直接后继）s，用s来替换结点p，然后再删除此结点s，如下图所示。

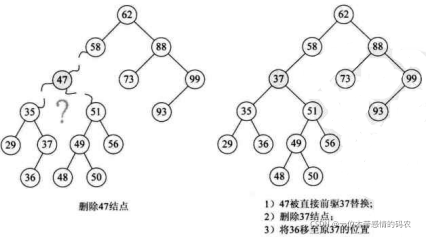
根据我们对删除结点三种情况的分析：

叶子结点；
仅有左或右子树的结点；
左右子树都有的结点，我们来看代码，下面这个算法是递归方式对二叉排序树T查找key，查找到时删除。

/* 若二叉排序树下中存在关键宇等于key的数据元素时，则删除该数据元素结点， */
/* 并返回TRUE;否则返回FALSE */
Status DeleteBST(BiTree *T,int key)
{
	if(!*T) /* 不存在关键宇等于key的数据元素 */
		return FALSE:
	else
	{
		if (key==(*T)->data)	/* 找到关键字等于key的数据元素 */
			return Delete(T);
		else if (key<(*T)->data)
			return DeleteBST(&(*T)->lchild, key);
		else
			return DeleteBST(G(*T)->rchild, key);
	}
}

这段代码和前面的二叉排序树查找几乎完全相同，唯一的区别就在于第 8 行，此时执行的是Delete方法，对当前结点进行删除操作。我们来看Delete的代码。

/* 从二又排序树中删除结点p，并重接它的左或右子树。 */
Status Delete(BiTree *p)
{
	BiTree q,s;
	if((*p)->rchild==NULL)	/* 右子树空则只需重接它的左子树 */
	{
		q=*p; *p=(*p)->lchild; free(q);
	}
	else if((*p)->1child==NULL)	/* 只需重接它的右子树 */
	{
		q=*p; *p=(*p)->rchild; free(q);
	}
	else	/* 左右于树均不空 */
	{
		q=*p; s=(*p)->lchild;
		while (s->rchild)	/* 转左，然后向右到尽头(找待删结点的前驱) */
		{
			q=s; s=s->rchild;
		}
		(*p)->data=s->data;	/* s指向被删结点的直接前驱 */
		if (q!=*p)
			q->rchild=s->lchild;	/* 重接q的右子树 */
		else
			q->lchild=s->lchild;	/* 重接q的左子树 */
		free(s);
	}
	return TRUE;
}

程序开始执行，代码第 4~7 行目的是为了删除没有右子树只有左子树的结点。此时只需将此结点的左孩子替换它自己，然后释放此结点内存，就等于删除了。
代码第 8~11 行是同样的道理处理只有右子树没有左子树的结点删除问题。
第 12~25 行处理复杂的左右子树均存在的问题。
第 14 行，将要删除的结点p赋值给临时的变量q，再将p的左孩子p->lchild赋值给临时的变量s。此时q指向 47 结点，s指向 35 结点，如下图所示。
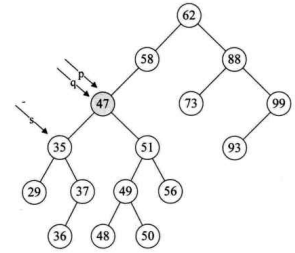
第 15~18 行，循环找到左子树的右结点，直到右侧尽头。就当前例子来说就是让q指向 35，而s指向了 37 这个再没有右子树的结点，如下图所示。
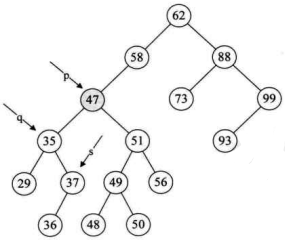
第 19 行，此时让要删除的结点p的位置的数据被赋值为s->data，即让p->data=37，如下图所示。
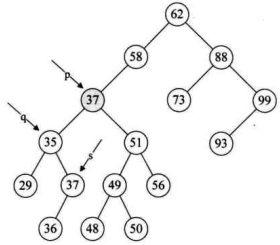
第 20~23 行，如果p和q指向不同，则将s->lchild赋值给q->rchild，否则就是将s->child赋值给q->lchild。显然这个例子p不等于q，将s->lchild指向的 36 赋值给q->rchild，也就是让q->rchild指向 36 结点，如下图所示。
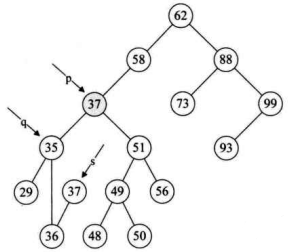
第 24 行，free(s)，就非常好理解了，将 37 结点删除，如下图所示。

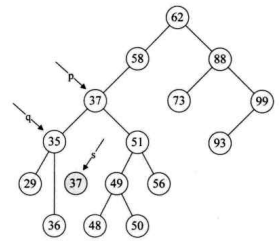
从这段代码也可以看出，我们其实是在找删除结点的前驱结点替换的方法，对于用后继结点来替换，方法上是一样的。

1.4 二叉排序树总结

总之，二叉排序树是以链接的方式存储，保持了链接存储结构在执行插入或删除操作时不用移动元素的优点，只要找到合适的插入和删除位置后，仅需修改链接指针即可。插入删除的时间性能比较好。而对于二叉排序树的查找，走的就是从根结点到要查找的结点的路径，其比较次数等于给定值的结点在二叉排序树的层数。极端情况，最少为 1 次，即根结点就是要找的结点，最多也不会超过树的深度。也就是说，二叉排序树的查找性能取决于二叉排序树的形状。可问题就在于，二叉排序树的形状是不确定的。
例如 {62,88,58,47,35,73,51,99,37,93} 这样的数组，我们可以构建如左下图的二叉排序树。但如果数组元素的次序是从小到大有序，如 {35,37,47,51,58,62,73,88,93,99}，则二叉排序树就成了极端的右斜树，注意它依然是一棵二叉排序树，如右下图。此时，同样是查找结点 99，左图只需要两次比较，而右图就需要 10 次比较才可以得到结果，二者差异很大。

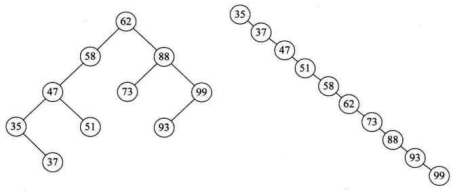
也就是说，我们希望二叉排序树是比较平衡的，即其深度与完全：二叉树相同，均为 $[log_2n]+1$ ，那么查找的时间复杂也就为 $O(logn)$ ，近似于折半查找，事实上，左上图也不够平衡，明显的左重右轻。
不平衡的最坏情况就是像右上图的斜树，查找时间复杂度为 $O(n)$ ，这等同于顺序查找。
因此，如果我们希望对一个集合按二叉排序树查找，最好是把它构建成一棵平衡的二叉排序树。这样我们就引申出另一个问题，如何让二叉排序树平衡的问题。