前言

部分内容摘自程杰的《大话数据结构》

1. 树

1.1 树的定义

之前我们一直在谈的是一对一的线性结构，可现实中，还有很多一对多的情况需要处理，所以我们需要研究这种一对多的数据结构——“树”，考虑它的各种特性，来解决我们在编程中碰到的相关问题。

树（Tree）是n (n≥0) 个结点的有限集。n=0时称为空树。在任意一棵非空树中：①有且仅有一个特定的称为根（Root）的结点；②当n>1时，其余结点可分为m (m>0) 个互不相交的有限集T $_1$ 、T $_2$ 、… 、T $_m$ ，其中每一个集合本身又是一棵树，并且称为根的子树（SubTree），如下图所示。

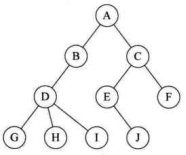
树的定义其实就是我们在讲解栈时提到的递归的方法。也就是在树的定义之中还用到了树的概念，这是一种比较新的定义方法。下图的子树 T $_1$ 和子树 T $_2$ 就是根结点A的子树。当然，D、G、H、I组成的树又是以B为根结点的子树，E、J组成的树是以C为根结点的子树。

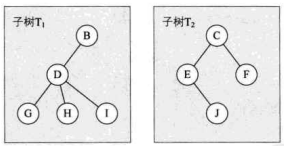
对于树的定义还需要强调两点：

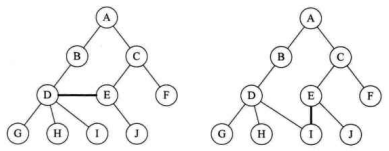
n>0时根结点是唯一的，不可能存在多个根结点，别和现实中的大树混在一起，现实中的树有很多根须，那是真实的树，数据结构中的树是只能有一一个根结点。
m>0时，子树的个数没有限制，但它们一定是互不相交的。像下图中的两个结构就不符合树的定义，因为它们都有相交的子树。

1.2 结点的分类

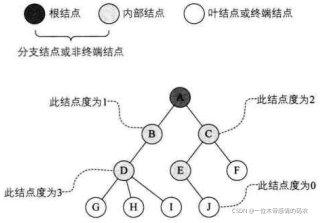
树的结点包含一个数据元素及若干指向其子树的分支。结点拥有的子树数称为结点的度（Degree）。度为0的结点称为叶结点（Leaf）或终端结点；度不为0的结点称为非终端结点或分支结点。除根结点之外，分支结点也称为内部结点。树的度是树内各结点的度的最大值。如下图所示，因为这棵树结点的度的最大值是结点D的度，为 3，所以树的度也为 3。

1.3 结点间的关系

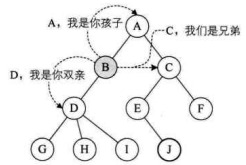
结点的子树的根称为该结点的孩子（Child），相应地，该结点称为孩子的双亲（Parent）。嗯，为什么不是父或母，叫双亲呢？呵呵，对于结点来说其父母同体，唯一的一个，所以只能把它称为双亲了。同一个双亲的孩子之间互称兄弟（Sibling）。结点的祖先是从根到该结点所经分支上的所有结点。所以对于H来说，D、 B、A都是它的祖先。反之，以某结点为根的子树中的任一结点都称为该结点的子孙。B的子孙有D、G、H、I，如下图所示。

1.4 树的其他相关概念

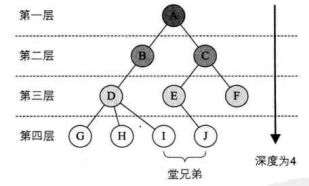
结点的层次（Level）从根开始定义起，根为第一层，根的孩子为第二层。若某结点在第l层，则其子树的根就在第l+1层。其双亲在同一层的结点互为堂兄弟。显然下图中的D、E、F是堂兄弟，而G、H、I、J也是堂兄弟。树中结点的最大层次称为树的深度（Depth）或高度，当前树的深度为 4。

如果将树中结点的各子树看成从左至右是有次序的，不能互换的，则称该树为有序树，否则称为无序树。
森林（Forest）是m (m≥0)棵互不相交的树的集合。对树中每个结点而言，其子树的集合即为森林。对于 1.1 节开头的图中的树而言，后面的图中的两棵子树 T $_1$ 和 T $_2$ 其实就可以理解为森林。
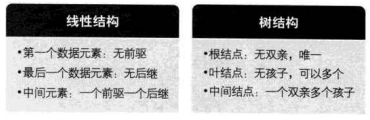
对比线性表与树的结构，它们有很大的不同，如下图所示。

2. 树的抽象数据类型

相对于线性结构，树的操作就完全不同了，这里我们给出一些基本和常用操作。

ADT 树(tree)
Data
	树是由一个根结点和若干棵子树构成。树中结点具有相同数据类型及层次关系。
Operation
	InitTree(*T)：构造空树T。
	DestroyTree(*T)：销毁树T。
	CreateTree(*T, definition)：按definition中給出树的定义来构造树。
	ClearTree(*T)：若树T存在，则将树T清为空树。
	TreeEmpty(T)：若T为空树，返回true,否则返回false。
	TreeDepth(T)：返回T的深度。
	Root(T)：返回T的根结点。
	value(T,cur e)：cur_e是树T中一个结点，返回此结点的值。
	Assign(T,cur e,value)：给树T的结点cur_e赋值为value。
	Parent(T,cur e)：若cur_e是树T的非根结点，则返回它的双亲，否则返回空。
	LeftChild(T,cur_ e)：若cur_e是树T的非叶结点，则返回它的最左孩子，否则返回空。
	RightSibling(T,cur_ e)：若cur_e有右兄弟，则返回它的右兄弟，否则返回空。
	InsertChild(*T, *p,i,c)：其中p指向树T的某个结点，i为所指结点p的度加上1,
							非空树c与T不相交，操作结果为插入c为树T中p指结点的第i棵子树。
	DeleteChild(*T,*p,i)：其中p指向树T的某个结点，i为所指结点p的度，操作
						结果为删除T中p所指结点的第i棵子树。
endADT

3. 树的存储结构

说到存储结构，就会想到我们前面博客讲过的顺序存储和链式存储两种结构。
先来看看顺序存储结构，用一段地址连续的存储单元依次存储线性表的数据元素。这对于线性表来说是很自然的，对于树这样一多对的结构呢？
树中某个结点的孩子可以有多个，这就意味着，无论按何种顺序将树中所有结点存储到数组中，结点的存储位置都无法直接反映逻辑关系，你想想看，数据元素挨个的存储，谁是谁的双亲，谁是谁的孩子呢？简单的顺序存储结构是不能满足树的实现要求的。
不过充分利用顺序存储和链式存储结构的特点，完全可以实现对树的存储结构的表示。我们这里要介绍三种不同的表示法“”双亲表示法、孩子表示法、孩子兄弟表示法。

3.1 双亲表示法

我们人可能因为种种原因，没有孩子，但无论是谁都不可能是从石头里蹦出来的，孙悟空显然不能算是人，所以是人一定会有父母。树这种结构也不例外，除了根结点外，其余每个结点，它不一定有孩子，但是一-定有且仅有一个双亲。
我们假设以一组连续空间存储树的结点，同时在每个结点中，附设一个指示器指示其双亲结点在数组中的位置。也就是说，每个结点除了知道自已是谁以外，还知道它的双亲在哪里。它的结点结构如下所示。

其中data是数据域，存储结点的数据信息。而parent是指针域，存储该结点的双亲在数组中的下标。
以下是我们的双亲表示法的结点结构定义代码：

/* 树的双亲表示法结点结构定义 */
#define MAX_TREE_SIZE 100

typedef int TElemType;	/* 树结点的数据类型，目前暂定为整型 */

typedef struct PTNode	/* 结点结构 */
{
	TElemType data;		/* 结点数据 */
	int parent;			/* 双亲位置 */
}PTNode;

typedef struct			/* 树结构 */
{
	PTNode nodes[MAX_TREE_SIZE];	/* 结点数组 */
	int r,n;						/* 根的位置和结点数 */
}PTree;

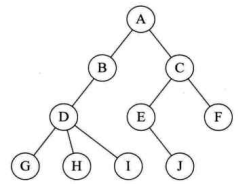
有了这样的结构定义，我们就可以来实现双亲表示法了。由于根结点是没有双亲的，所以我们约定根结点的位置域设置为 -1，这也就意味着，我们所有的结点都存有它双亲的位置。如下图中的树结构和下表中的树双亲表示所示。

下标	data	parent
0	A	-1
1	B	0
2	C	0
3	D	1
4	E	2
5	F	2
6	G	3
7	H	3
8	I	3
9	J	4

这样的存储结构，我们可以根据结点的parent指针很容易找到它的双亲结点，所用的时间复杂度为O(1)，直到parent为 -1 时，表示找到了树结点的根。可如果我们要知道结点的孩子是什么，对不起，请遍历整个结构才行。
这真是麻烦，能不能改进一下呢？
当然可以。我们增加一个结点最左边孩子的域，不妨叫它长子域，这样就可以很容易得到结点的孩子。如果没有孩子的结点，这个长子域就设置为 -1，如下表所示。

下标	data	parent	firstchild
0	A	-1	1
1	B	0	3
2	C	0	4
3	D	1	6
4	E	2	-1
5	F	2	-1
6	G	3	-1
7	H	3	-1
8	I	3	-1
9	J	4	-1

对于有 0 个或 1 个孩子结点来说，这样的结构是解决了要找结点孩子的问题了。甚至是有 2 个孩子，知道了长子是谁，另一个当然就是次子了。
另外一个问题场景，我们很关注各兄弟之间的关系，双亲表示法无法体现这样的关系，那我们怎么办？嗯，可以增加一个右兄弟域来体现兄弟关系，也就是说，每一个结点如果它存在右兄弟，则记录下右兄弟的下标。同样的，如果右兄弟不存在，则赋值为 -1，如下表所示。

下标	data	parent	firstchild
0	A	-1	-1
1	B	0	2
2	C	0	-1
3	D	1	-1
4	E	2	5
5	F	2	-1
6	G	3	7
7	H	3	8
8	I	3	-1
9	J	4	-1

但如果结点的孩子很多，超过了 2 个。我们又关注结点的双亲、又关注结点的孩子、还关注结点的兄弟，而且对时间遍历要求还比较高，那么我们还可以把此结构扩展为有双亲域、长子域、再有右兄弟域。存储结构的设计是一个非常灵活的过程。一个存储结构设计得是否合理，取决于基于该存储结构的运算是否适合、是否方便，时间复杂度好不好等。注意也不是越多越好，有需要时再设计相应的结构。复杂的结构意味着更多时间与空间的开销，简单的设计对应着快速的查找与增删，我们确实要根据实际情况来做出取舍。

3.2 孩子表示法

换一种完全不同的考虑方法。由于树中每个结点可能有多棵子树，可以考虑用多重链表，即每个结点有多个指针城，其中每个指针指向一棵子树的根结点,我们把这种方法叫做多重链表表示法。不过，树的每个结点的度，也就是它的孩子个数是不同的。所以可以设计两种方案来解决。

方案一

一种是指针城的个数就等于树的度，复习一下，树的度是树各个结点度的最大值。其结构如下表所示。

其中data是数据域：child1~childd是指针域，用来指向该结点的孩子结点。
对于下图的树来说，树的度是 3，所以我们的指针域的个数是 3，这种方法实现如下图所示。

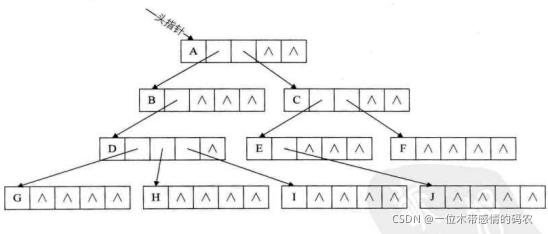
这种方法对于树中各结点的度相差很大时，显然是很浪费空间的，因为有很多的结点，它的指针域都是空的。不过如果树的各结点度相差很小时，那就意味着开辟的空间被充分利用了，这时存储结构的缺点反而变成了优点。
既然很多指针域都可能为空，为什么不按需分配空间呢？于是我们有了第二种方案。

方案二

第二种方案每个结点指针域的个数等于该结点的度，我们专门取一个位置来存储结点指针域的个数，其结构如下表所示。

其中data为数据域，degree为度域，也就是存储该结点的孩子结点的个数；child1~childd为指针域，指向该结点的各个孩子的结点。
对于方案一图中的树来说，这种方法实现如下图所示。

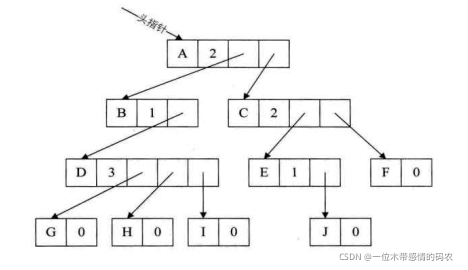
这种方法克服了浪费空间的缺点，对空间利用率是很高了，但是由于各个结点的链表是不相同的结构，加上要维护结点的度的数值，在运算上就会带来时间上的损耗。
能否有更好的方法，既可以减少空指针的浪费又能使结点结构相同。
仔细观察，我们为了要遍历整棵树，把每个结点放到一个顺序存储结构的数组中是合理的，但每个结点的孩子有多少是不确定的，所以我们再对每个结点的孩子建立一个单链表体现它们的关系。
这就是我们要讲的孩子表示法。具体办法是，把每个结点的孩子结点排列起来，以单链表作存储结构，则n个结点有n个孩子链表，如果是叶子结点则此单链表为空。然后n个头指针又组成一个线性表，采用顺序存储结构，存放进一个一维数组中，如下图所示。

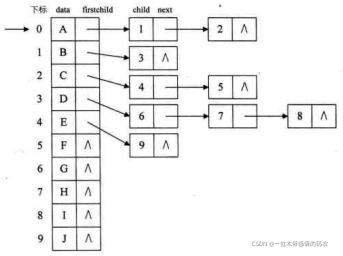
为此，设计两种结点结构，一个是孩子链表的孩子结点，如下表所示。

其中child是数据域，用来存储某个结点在表头数组中的下标；next是指针域，用来存储指向某结点的下一个孩子结点的指针。
另一个是表头数组的表头结点，如下表所示。

其中data是数据域，存储某结点的数据信息。frstchild是头指针域，存储该结点的孩子链表的头指针。
以下是我们的孩子表示法的结构定义代码。

/* 树的孩子表示法结构定义 */
#define MAX_TREE_SIZE 100

typedef int TRlemType;	/* 树节点的数据类型，目前暂定为整型 */

typedef struct CTNode	/* 孩子结点 */
{
	int child;
	struct CTNode *next;
} *ChildPtr;

typedef struct	/* 表头结构 */
{
	TElemType data ;
	ChildPtr firstchild;
} CTBox:
typedef struct	/* 树结构 */
{
	CTBox nodes[MAX_TREE_SIZE];	/* 结点数组 */
	int r,n;					/* 根的位置和结点数 */
} CTree;

这样的结构对于我们要查找某个结点的某个孩子，或者找某个结点的兄弟，只需要查找这个结点的孩子单链表即可。对于遍历整棵树也是很方便的，对头结点的数组循环即可。
但是，这也存在着问题，我如何知道某个结点的双亲是谁呢？比较麻烦，需要整棵树遍历才行，难道就不可以把双亲表示法和孩子表示法综合一下吗？当然是可以。如下图所示。

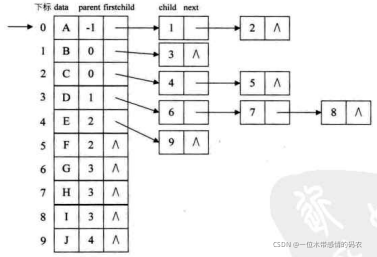
我们把这种方法称为双亲孩子表示法，应该算是孩子表示法的改进。至于这个表示法的具体结构定义，这里就略过，感兴趣的朋友们可以自己去设计了。

3.3 孩子兄弟表示法

刚才我们分别从双亲的角度和从孩子的角度研究树的存储结构，如果我们从树结点的兄弟的角度又会如何呢？当然，对于树这样的层级结构来说，只研究结点的兄弟是不行的，我们观察后发现，任意一棵树，它的结点的第一个孩子如果存在就是唯一的，它的右兄弟如果存在也是唯一-的。因此，我们设置两个指针，分别指向该结点的第一个孩子和此结点的右兄弟。
结点结构如下表所示。

其中data是数据域，firstchild为指针域，存储该结点的第一个孩子结点的存储地址；rightib是指针域，存储该结点的右兄弟结点的存储地址。
结构定义代码如下：

/* 树的孩子兄弟表示法结构定义 */
typedef struct CSNode
{
	TElenType data;
	struct CSNode *firstchild,*rightsib;
} CSNode,*CSTree;

对于上图的树来说，这种方法实现的示意图如下图所示。

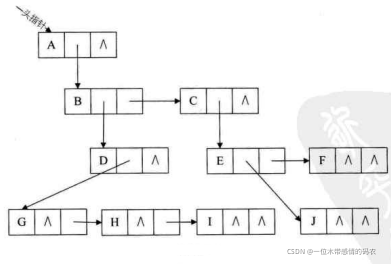
这种表示法，给查找某个结点的某个孩子带来了方便，只需要通过fistchild找到此结点的长子，然后再通过长子结点的rightib找到它的二弟，接着一直下去，直到找到具体的孩子。当然，如果想找某个结点的双亲，这个表示法也是有缺陷的，那怎么办呢？
呵呵，对，如果真的有必要，完全可以再增加一个parent指针域来解决快速查找双亲的问题，这里就不再细谈了。
其实这个表示法的最大好处是它把一棵复杂的树变成了一棵二叉树。我们把上图变形就成了下图这个样子。

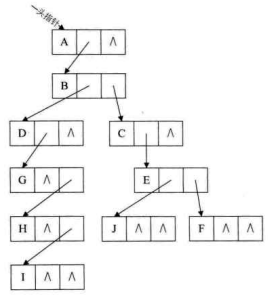
这样就可以充分利用二叉树的特性和算法来处理这棵树了。在下一篇博客中，再详细讲讲二叉树是什么。

4. 总结

本篇提到了树的定义，讲到了递归在树定义中的应用。提到了如子树、结点、度、叶子、分支结点、双亲、孩子、层次、深度、森林等诸多概念，这些都是需要在理解的基础上去记忆的。
我们谈到了树的存储结构时，讲了双亲表示法、孩子表示法、孩子兄弟表示法等不同的存储结构。并由孩子兄弟表示法引出了我们这块最重要一种树，二叉树。
对于二叉树的详解，在下一篇博客中再继续讲解。