《数据结构与算法》（七）- 队列详解

前言

部分内容摘自程杰的《大话数据结构》

1. 队列的定义

  相信大家在用电脑时都经历过，机器有时会处于疑似死机的状态，鼠标点什么似乎都没用，双击任何快捷方式都不动弹。就当你失去耐心，打算 reset 时。突然它像酒醒了一样， 把你刚才点击的所有操作全部都按顺序执行了一遍。这其实是因为操作系统中的多个程序因需要通过一个通道输出，而按先后次序排队等待造成的。
  再比如像移动、联通、电信等客服电话，客服人员与客户相比总是少数，在所有的客服人员都占线的情况下，客户会被要求等待，直到有某个客服人员空下来，才能让最先等待的客户接通电话。这里也是将所有当前拨打客服电话的客户进行了排队处理。
  操作系统和客服系统中，都是应用了一种数据结构来实现刚才提到的先进先出的排队功能，这就是队列。

队列（queue）是只允许在一端进行插入操作，而在另一端进行删除操作的线性表。

  队列是一种先进先出（First In First Out）的线性表，简称 FIFO。允许插入的一端称为队尾，允许删除的一端称为队头。 假设队列是 q=(a$_1$, a$_2$, … a$_n$)，那么 a$_1$ 就是队头元素，而 a$_n$ 是队尾元素。这样我们就可以删除时，总是从 a$_1$ 开始，而插入时，列在最后。这也比较符合我们通常生活中的习惯，排在第一个的优先出列，最后来的当然排在队伍最后，如下图所示。

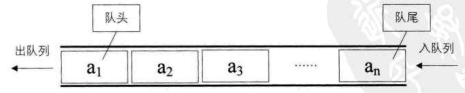
  队列在程序设计中用得非常频繁。前面我们已经举了两个例子，再比如用键盘进行各种字母或数字的输入，到显示器上如记事本软件上的输出，其实就是队列的典型应用，假如你本来和女友聊天，想表达你是我的上帝，输入的是 god，而屏幕上却显示出了 dog 发了出去，这真是要气死人了。

2. 队列的抽象数据类型

  同样是线性表，队列也有类似线性表的各种操作，不同的就是插入数据只能在队尾进行，删除数据只能在队头进行。

ADT 队列(Queue)
Data
	同线性表。元素具有相同的类型，相邻元素具有前驱和后继关系。
Operation
	InitQueue(*Q)：初始化操作，建立一个空队列Q。
	DestroyQueue(*Q)：若队列Q存在，则销毁它。
	ClearQueue(*Q)：将队列Q清空。
	QueueEmpty(Q)：若队列Q为空，返回true,否则返回false。
	GetHead(Q,*e)：若队列Q存在且非空，用e返回队列Q的队头元素。
	EnQueue(*Q,e)：若队列Q存在，插入新元素e到队列Q中并成为队尾元素。
	DeQueue(*Q,*e)：删除队列Q中队头元素，并用e返回其值。
	QueueLength(Q)：返回队列Q的元素个数
endADT

3. 循环队列

  线性表有顺序存储和链式存储，栈是线性表，所以有这两种存储方式。同样，队列作为一种特殊的线性表，也同样存在这两种存储方式。我们先来看队列的顺序存储结构。

3.1 队列顺序存储的不足

  我们假设一个队列有n个元素，则顺序存储的队列需建立一个大于n的数组，并把队列的所有元素存储在数组的前n个单元，数组下标为 0 的一端即是队头。所谓的入队列操作，其实就是在队尾追加一个元素，不需要移动任何元素，因此时间复杂度为O(1)，如下图所示。

  与栈不同的是，队列元素的出列是在队头，即下标为 0 的位置，那也就意味着，队列中的所有元素都得向前移动，以保证队列的队头，也就是下标为 0 的位置不为空，此时时间复杂度为O(n)，如下图所示。

  这里的实现和线性表的顺序存储结构完全相同，不再详述。
  在现实中也是如此，一群人在排队买票，前面的人买好了离开，后面的人就要全部向前一步，补上空位，似乎这也没什么不好。
  可有时想想，为什么出队列时一定要全部移动呢，如果不去限制队列的元素必须存储在数组的前n个单元这一条件，出队的性能就会大大增加。也就是说，队头不需要一定在下标为 0 的位置，如下图所示。

  为了避免当只有一个元素时，队头和队尾重合使处理变得麻烦，所以引入两个指针，front指针指向队头元素，rear指针指向队尾元素的下一个位置，这样当front等于rear时，此队列不是还剩一个元素，而是空队列。
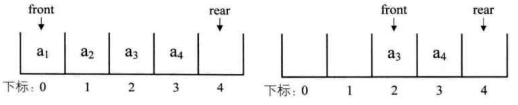
  假设是长度为 5 的数组，初始状态，空队列如下图的左图所示，front与rear指针均指向下标为 0 的位置。然后入队 a$_1$、a$_2$、a$_3$、a$_4$，front指针依然指向下标为 0 位置，而rear指针指向下标为 4 的位置，如下图的右图所示。

  出队a$_1$、a$_2$，则front指针指向下标为 2 的位置，rear不变，如下图的左图所示，再入队a$_s$，此时front指针不变，rear指针移动到数组之外。嗯？数组之外，那将是哪里？如下图的右图所示。

  问题还不止于此。假设这个队列的总个数不超过 5 个，但目前如果接着入队的话，因数组末尾元素已经占用，再向后加，就会产生数组越界的错误，可实际上，我们的队列在下标为 0 和 1 的地方还是空闲的。我们把这种现象叫做 “假溢出”。
  现实当中，你上了公交车，发现前排有两个空座位，而后排所有座位都已经坐满，你会怎么做？立马下车，并对自己说，后面没座了，我等下一辆？
  没有这么笨的人，前面有座位，当然也是可以坐的，除非坐满了，才会考虑下一辆。

3.2 循环队列定义

  所以解决假溢出的办法就是后面满了，就再从头开始，也就是头尾相接的循环。我们把队列的这种头尾相接的顺序存储结构称为循环队列。
  刚才的例子继续，上图的rear可以改为指向下标为 0 的位置，这样就不会造成指针指向不明的问题了，如下图所示。

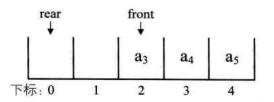
  接着入队 a$_6$，将它放置于下标为 0 处，rear指针指向下标为 1 处，如下图的左图所示。若再入队 a$_7$，则rear指针就与front指针重合，同时指向下标为 2 的位置，如下图的右图所示。

• 此时问题又出来了， 我们刚才说，空队列时，front等于rear，现在当队列满时，也是front等于rear，那么如何判断此时的队列究竟是空还是满呢？
• 办法一是设置一个标志变量flag，当front=rear，且flag=0时为队列空，当front=rear，且flag=1时为队列满。
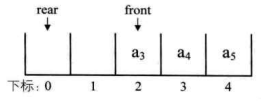
• 办法二是当队列空时，条件就是front=rear，当队列满时，我们修改其条件，保留一个元素空间。也就是说，队列满时，数组中还有一个空闲单元。例如下图所示，我们就认为此队列已经满了，也就是说，我们不允许下图的右图情况出现。

  我们重点来讨论第二种方法，由于rear可能比front大，也可能比front小，所以尽管它们只相差一个位置时就是满的情况，但也可能是相差整整一圈。 所以若队列的最大尺寸为QueueSize，那么队列满的条件是（rear+1）QueueSize == front（取模 “%” 的目的就是为了整合rear与front大小为一个问题）。比如上面这个例子，QueueSize=5，上图的左图中front=0，而rear=4，(4+1)%5= 0，所以此时队列满。再比如上图中的右图，front=2而rear=1。(1 + 1)%5=2，所以此时队列也是满的。而对于下图，front=2而rear=0，(0+1)%5=1，1≠2，所以此时队列并没有满。

  另外，当rear>front时，即下图的左图和下图的右图，此时队列的长度为rear-front。 但当rear<front时，如上图和上上图的左图，队列长度分为两段，一段是QueueSize-front，另一段是0+rear，加在一起，队列长度为rear-front+QueueSize。
  因此通用的计算队列长度公式为：
  (rear- front + QueueSize) %QueueSize
  有了这些讲解，现在实现循环队列的代码就不难了。

  循环队列的顺序存储结构代码如下：

typedef int QElemType;	/* QElemType类型根据实际情况而定，这里假设为int */
/* 循环队列的顺序存储结构 */
typedef struct
{
	QElemType data[MAXSIZE];
	int front;	/* 头指针 */
	int rear;	/* 尾指针，若队列不空，指向队列尾元素的下一个位置 */
} SqQueue;

  循环队列的初始化代码如下：

/* 初始化一个空队列Q */
Status InitQueue(SqQueue *Q)
{
	Q->front=0;
	Q->rear=0;
	return OK;
}

  循环队列求队列长度代码如下：

/* 返回Q的元素个数，也就是队列的当前长度 */
int QueueLength(SqQueue Q)
{
	return (Q.rear - Q.front + MAXSIZE) % MAXSIZE;
}

  循环队列的入队列操作代码如下：

/* 若队列未满，则插入元素e为Q新的队尾元素 */
Status EnQueue(SqQueue *Q,QE1emType e)
{
	if ((Q->rear+1)%SMAXSIZE == Q->front)	/* 队列满的判断 */
		return ERROR;
	Q->data[Q->rear]=e;	/* 将元素e赋值给队尾 */
	Q->rear=(Q->rear+1)%MAXSIZE;	/* rear指针向后移一位置 */
									/* 若到最后则转到数组头部 */
	return OK;
}

  循环队列的出队列操作代码如下：

/* 若队列不空，则删除Q中队头元素，用e返回其值 */
Status DeQueue(SqQueue *Q,QE1emType *e)
{
	if (Q->front == Q->front)	/* 队列空的判断 */
		return ERROR;
	*e=Q->data[Q->front];	/* 将队头元素赋值给e */
	Q->front=(Q->front+1)%MAXSIZE;	/* front指针向后移一位置 */
									/* 若到最后则转到数组头部 */
	return OK;
}

  从这一段讲解，大家应该发现，单是顺序存储，若不是循环队列，算法的时间性能是不高的，但循环队列又面临着数组可能会溢出的问题，所以我们还需要研究一下不需要担心队列长度的链式存储结构。

4. 队列的链式存储结构及实现

  队列的链式存储结构，其实就是线性表的单链表，只不过它只能尾进头出而已，我们把它简称为链队列。 为了操作上的方便，我们将队头指针指向链队列的头结点，而队尾指针指向终端结点，如下图所示。

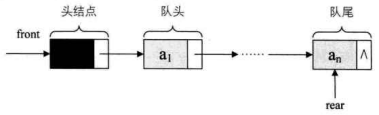
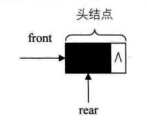
  空队列时，front和rear都指向头结点，如下图所示。

  链队列的结构为：

typedef int QElemType; /* QElemType类型根据实际情况而定，这里假设为int */

typedef struct QNode	/* 结点结构 */
{
	QElemType data;
	struct QNode *next;
}QNode, QueuePtr;

typedef struct	/* 队列的链表结构 */
{
	QueuePtr front,rear;	/* 队头、队尾指针 */
}LinkQueue;

4.1 队列的链式存储结构——入队操作

  入队操作时，其实就是在链表尾部插入结点，如下图所示。

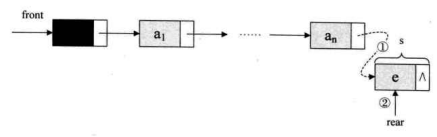
  其代码如下：

/* 插入元素e为Q的新的队尾元素 */
Status EnQueue(LinkQueue *, QElemType e)
{
	QueuePtr s=(QueuePtr)malloc(sizeof(QNode));
	if (!s)	/* 存储分配失败 */
		exit (OVERFLOW);
	s->data=e;
	s->next=NULL;
	Q->rear->next=s;	/* 把拥有元素e新结点s赋值给原队尾结点的后继,见上图中① */
	Q->rear=s;	/* 把当前的s设置为队尾结点，rear指向s，见上图中② */
	return OK;
}

4.2 队列的链式存储结构——出队操作

  出队操作时，就是头结点的后继结点出队，将头结点的后继改为它后面的结点，若链表除头结点外只剩一个元素时，则需将rear指向头结点，如下图所示。

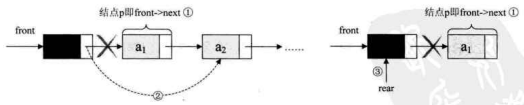
  代码如下：

/* 若队列不空，删除Q的队头元素，用e返回其值，并返回OK，否则返回ERROR */
Status DeQueue(LinkQueue *Q, QElemType *e)
{
	QueuePtr p;
	if (Q->front==Q->rear )
		return ERROR:
	p=Q->front->next;		/* 将欲删除的队头结点暂存给p,见上图中① */
	*e=p->data;				/* 将欲删除的队头结点的值赋值给e */
	0->front->next=p->next;	/* 将原队头结点后继p->next赋值给头结点后继，见上图中② */
	if (Q->rear==p)			/* 若队头是队尾，则删除后将rear指向头结点，见上图中③ */
		Q->rear=Q->front;
	free(p);
	return OK;
}

  对于循环队列与链队列的比较，可以从两方面来考虑，从时间上，其实它们的基本操作都是常数时间，即都为 O(1) 的， 不过循环队列是事先申请好空间，使用期间不释放，而对于链队列，每次申请和释放结点也会存在一些时间开销，如果入队出队频繁，则两者还是有细微差异。对于空间上来说，循环队列必须有一个固定的长度，所以就有了存储元素个数和空间浪费的问题。而链队列不存在这个问题，尽管它需要一个指针域，会产生一些空间上的开销，但也可以接受。所以在空间上，链队列更加灵活。
  总的来说，在可以确定队列长度最大值的情况下，建议用循环队列，如果你无法预估队列的长度时，则用链队列。

5. 总结

  栈和队列，它们都是特殊的线性表，只不过对插入和删除操作做了限制。
  栈（stack）是限定仅在表尾进行插入和删除操作的线性表。
  队列（queue）是只允许在一端进行插入操作， 而在另一端进行删除操作的线性表。
  它们均可以用线性表的顺序存储结构来实现，但都存在着顺序存储的一些弊端。因此它们各自有各自的技巧来解决这个问题。
  对于栈来说，如果是两个相同数据类型的栈，则可以用数组的两端作栈底的方法来让两个栈共享数据，这就可以最大化地利用数组的空间。
  对于队列来说，为了避免数组插入和删除时需要移动数据，于是就引入了循环队列，使得队头和队尾可以在数组中循环变化。解决了移动数据的时间损耗，使得本来插入和删除是 O(n) 的时间复杂度变成了O(1)。
它们也都可以通过链式存储结构来实现，实现原则上与线性表基本相同如下图所示。