《数据结构与算法》(二)- 算法详解
前言
部分内容摘自程杰的《大话数据结构》
1. 数据结构与算法的关系
数据结构为算法提供服务,算法围绕数据结构操作。
- 数据结构只是静态的描述了数据元素之间的关系。
- 高效的程序需要在数据结构的基础上设计和选择算法。
程序=数据结构+算法
2. 两种算法的比较
用C语言实现一个求1+2+3+·····+100的程序:
1 | int i, sum = 0, n = 100; |
这是最简单的计算机程序之一,它就是一种算法,我不去解释这代码的含义了。问题在于,你的第一直觉是这样写的,但这样是不是真的很好?是不是最高效?
还有另一种比这更快的方法:
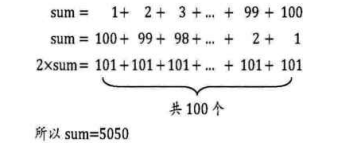
用程序来实现如下:
1 | int sum = 0,n = 100; |
这种方法相当于另一种求等差数列的算法,不仅仅可以用于1加到100,就是加到一千、一万、一亿(需要更改整型变量类型为长整型,否则会溢出),也就是瞬间之事。但如果用刚才的程序,显然计算机要循环一千、一万、一亿次的加法运算。人脑比电脑算得快,似乎成为了现实。
3. 算法的定义
算法是解决特定问题求解步骤的描述,在计算机中表现为指令的有限序列,并且每条指令表示一个或多个操作。
现实世界中的问题千奇百怪,算法当然也就千变万化,没有通用的算法可以解决所有的问题。甚至解决一个小问题,很优秀的算法却不一定适合它。
算法定义中,提到了指令,指令能被人或机器等计算装置执行。它可以是计算机指令,也可以是我们平时的语言文字。
4. 算法的特性
算法具有五个基本特性:输入、输出、有穷性、确定性和可行性。
4.1 输入输出
输入和输出特性比较容易理解,算法具有零个或多个输入。尽管对于绝大多数算法来说,输入参数都是必要的,但对于个别情况,如打印“hello world!”这样的代码,不需要任何输入参数,因此算法的输入可以是零个。算法至少有一个或多个输出,算法是一定需要输出的,不需要输出,你用这个算法干吗?输出的形式可以是打印输出,也可以是返回一个或多个值等。
4.2 有穷性
有穷性指算法在执行有限的步骤之后,自动结束而不会出现无限循环,并且每一个步骤在可接受的时间内完成。 现实中经常会写出死循环的代码,这就是不满足有穷性。当然这里有穷的概念并不是纯数学意义的,而是在实际应用当中合理的、可以接受的“有边界”。你说你写一个算法,计算机需要算上个二十年,一定会结束,它在数学意义上是有穷了,可是媳妇都熬成婆了,算法的意义也就不大了。
4.3 确定性
确定性:算法的每一步骤都具有确定的含义,不会出现二义性。 算法在一定条件下,只有一条执行路径,相同的输入只能有唯一的输出结果。算法的每个步骤被精确定义而无歧义。
4.4 可行性
可行性:算法的每一步都必须是可行的,也就是说,每一步都能够通过执行有限次数完成。 可行性意味着算法可以转换为程序上机运行,并得到正确的结果。尽管在目前计算机界也存在那种没有实现的极为复杂的算法,不是说理论上不能实现,而是因为过于复杂,我们当前的编程方法、工具和大脑限制了这个工作,不过这都是理论研究领域的问题,不属于我们现在要考虑的范围。
5. 算法设计的要求
5.1 正确性
正确性:算法的正确性是指算法至少应该具有输入、输出和加工处理无歧义性、能正确反映问题的需求、能够得到问题的正确答案。
但是算法的“正确”通常在用法上有很大的差别,大体分为以下四个层次:
- 算法程序没有语法错误。
- 算法程序对于合法的输入数据能够产生满足要求的输出结果。
- 算法程序对于非法的输入数据能够得出满足规格说明的结果。
- 算法程序对于精心选择的,甚至刁难的测试数据都有满足要求的输出结果。
对于这四层含义,层次 1 要求最低,但是仅仅没有语法错误实在谈不上是好算法。这就如同仅仅解决温饱,不能算是生活幸福一样。而层次 4 是最困难的,我们几乎不可能逐一验证所有的输入都得到正确的结果。
因此算法的正确性在大部分情况下都不可能用程序来证明,而是用数学方法证明的。证明一个复杂算法在所有层次上都是正确的,代价非常昂贵。所以一般情况下,我们把层次 3 作为个算法是否正确的标准。
5.2 可读性
可读性:算法设计的另一目的是为了便于阅读、理解和交流。
可读性高有助于人们理解算法,晦涩难懂的算法往往隐含错误,不易被发现,并且难于调试和修改。
我们写代码的目的,一方面是为了让计算机执行,但还有一个重要的目的是为了便于他人阅读,让人理解和交流,自己将来也可能阅读,如果可读性不好,时间长了自己都不知道写了些什么。可读性是算法(也包括实现它的代码)好坏很重要的标志。
5.3 健壮性
一个好的算法还应该能对输入数据不合法的情况做合适的处理。比如输入的时间或者距离不应该是负数等。
健壮性:当输入数据不合法时,算法也能做出相关处理,而不是产生异常或莫名其妙的结果。
5.4 时间效率高和存储量低
最后,好的算法还应该具备时间效率高和存储量低的特点。
时间效率指的是算法的执行时间。对于同一个问题,如果有多个算法能够解决,执行时间短的算法效率高,执行时间长的效率低。存储量需求指的是算法在执行过程中需要的最大存储空间,主要指算法程序运行时所占用的内存或外部硬盘存储空间。设计算法应该尽量满足时间效率高和存储量低的需求。 在生活中,人们都希望花最少的钱,用最短的时间,办最大的事,算法也是一样的思想,最好用最少的存储空间,花最少的时间,办成同样的事就是好的算法。求100个人的高考成绩平均分,与求全省的所有考生的成绩平均分在占用时间和内存存储上是有非常大的差异的,我们自然是追求可以高效率和低存储量的算法来解决问题。
综上,好的算法,应该具有正确性、可读性、健壮性、高效率和低存储量的特征。
6. 算法效率的度量方法
6.1 事后统计法
事后统计方法:这种方法主要是通过设计好的测试程序和数据,利用计算机计时器对不同算法编制的程序的运行时间进行比较,从而确定算法效率的高低。
但这种方法显然是有很大缺陷的:
- 必须依据算法事先编制好程序,这通常需要花费大量的时间和精力。如果编制出来发现它根本是很糟糕的算法,不是竹篮打水一场空吗?
- 时间的比较依赖计算机硬件和软件等环境因素,有时会掩盖算法本身的优劣。要知道,现在的一台四核处理器的计算机,跟当年286、386、486等老爷爷辈的机器相比,在处理算法的运算速度上,是不能相提并论的;而所用的操作系统、编译器、运行框架等软件的不同,也可以影响它们的结果;就算是同一台机器,CPU使用率和内存占用情况不一样,也会造成细微的差异。
- 算法的测试数据设计困难,并且程序的运行时间往往还与测试数据的规模有很大关系,效率高的算法在小的测试数据面前往往得不到体现。比如 10 个数字的排序,不管用什么算法,差异几乎是零。而如果有一百万个随机数字排序,那不同算法的差异就非常大了。那么我们为了比较算法,到底用多少数据来测试,这是很难判断的问题。
基于事后统计方法有这样那样的缺陷,我们考虑不予采纳。
6.2 事前分析估算法
事前分析估算方法:在计算机程序编制前,依据统计方法对算法进行估算。
经过分析,我们发现,一个用高级程序语言编写的程序在计算机上运行时所消耗的时间取决于下列因素:
- 算法采用的策略、方法。
- 编译产生的代码质量。
- 问题的输入规模。
- 机器执行指令的速度。
第 1 条当然是算法好坏的根本,第 2 条要由软件来支持,第 4 条要看硬件性能。也就是说,抛开这些与计算机硬件、软件有关的因素,一个程序的运行时间,依赖于算法的好坏和问题的输入规模。所谓问题输入规模是指输入量的多少。
我们来看看前面举的例子,两种求和的算法:
第一种算法:
1 | int i, sum = 0, n = 100; /* 执行1次 */ |
第二种算法:
1 | int sum = 0,n = 100; /* 执行1次 */ |
显然,第一种算法,执行了1+(n+1) +n+1次=2n+3次;而第二种算法,是1+1+1=3次。事实上两个算法的第一条和最后一条语句是一样的,所以我们关注的代码其实是中间的那部分,我们把循环看作一个整体,忽略头尾循环判断的开销,那么这两个算法其实就是n次与1次的差距。算法好坏显而易见。
我们再来延伸一下上面这个句子:
1 | int i, j, x = 0, sum = 0, n = 100; /* 执行1次 */ |
这个例子中,i从 1 到 100,每次都要让j循环 100 次,而当中的x++和 sum =sum + x;其实就是1+2+3+……+10000,也就是 100^2^ 次,所以这个算法当中,循环部分的代码整体需要执行 n^2^(忽略循环体头尾的开销)次。显然这个算法的执行次数对于同样的输入规模n = 100,要多于前面两种算法,这个算法的执行时间随着n的增加也将远远多于前面两个。
此时你会看到,测定运行时间最可靠的方法就是计算对运行时间有消耗的基本操作的执行次数。运行时间与这个计数成正比。
我们不关心编写程序所用的程序设计语言是什么,也不关心这些程序将跑在什么样的计算机中,我们只关心它所实现的算法。这样,不计那些循环索引的递增和循环终止条件、变量声明、打印结果等操作,最终,在分析程序的运行时间时,最重要的是把程序看成是独立于程序设计语言的算法或一系列步骤。
可以从问题描述中得到启示,同样问题的输入规模是n,求和算法的第一种,求1+2+…+n需要一段代码运行n次。那么这个问题的输入规模使得操作数量是f(n)= n,显然运行 100 次的同一段代码规模是运算 10 次的 10 倍。而第二种,无论n为多少,运行次数都为 1,即f(n)=1;第三种,运算100次是运算 10 次的 100 倍。因为它是f(n)=n^2^。
我们在分析一个算法的运行时间时,重要的是把基本操作的数量与输入规模关联起来,即基本操作的数量必须表示成输入规模的函数。
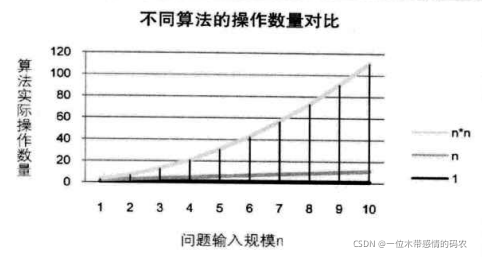
我们可以这样认为,随着n值的越来越大,它们在时间效率上的差异也就越来越大。
7. 函数的渐进增长
我们现在来判断一下,两个算法A和B哪个更好。假设两个算法的输入规模都是n,算法A要做2n+3次操作,你可以理解为先有一个n次的循环,执行完成后,再有一个n次循环,最后有三次赋值或运算,共2n+3次操作。算法B要做3n+1次操作。你觉得它们谁更快呢?
准确说来,答案是不一定的:
| 次数 | 算法A(2n+3) | 算法A'(2n) | 算法B(3n+1) | 算法B'(3n) |
|---|---|---|---|---|
| n = 1 | 5 | 2 | 4 | 3 |
| n = 2 | 7 | 4 | 7 | 6 |
| n = 3 | 9 | 6 | 10 | 9 |
| n = 10 | 23 | 20 | 31 | 30 |
| n = 100 | 203 | 200 | 301 | 300 |
当n =1时,算法A效率不如算法B(次数比算法B要多一次)。而当n=2时,两者效率相同;当n>2时,算法A就开始优于算法B了,随着n的增加,算法A比算法B越来越好了(执行的次数比B要少)。于是我们可以得出结论,算法A总体上要好过算法B。
此时我们给出这样的定义,输入规模n在没有限制的情况下,只要超过一个数值N,这个函数就总是大于另一个函数,我们称函数是渐近增长的。
函数的渐近增长:给定两个函数 f(n) 和 g(n),如果存在一个整数N,使得对于所有的n>N, f(n)总是比g(n)大,那么,我们说f(n)的增长渐近快于g(n)。
从中我们发现,随着n的增大,后面的+3还是+1其实是不影响最终的算法变化的,例如算法A’与算法B’,所以,我们可以忽略这些加法常数。后面的例子,这样的常数被忽略的意义可能会更加明显。
我们来看第二个例子,算法C是4n+8,算法D是2n2+1:
| 次数 | 算法C(4n+8) | 算法C'(4n) | 算法D(2n^2+1) | 算法D'(n^2) |
|---|---|---|---|---|
| n = 1 | 12 | 1 | 3 | 1 |
| n = 2 | 16 | 2 | 9 | 4 |
| n = 3 | 20 | 3 | 19 | 9 |
| n = 10 | 48 | 10 | 201 | 100 |
| n = 100 | 408 | 100 | 20001 | 10000 |
| n = 1000 | 4008 | 1000 | 2000001 | 1000000 |
当n≤3的时候,算法C要差于算法D(因为算法C次数比较多),但当n>3后,算法C的优势就越来越优于算法D了,到后来更是远远胜过。而当后面的常数去掉后,我们发现其实结果没有发生改变。甚至我们再观察发现,哪怕去掉与n相乘的常数,这样的结果也没发生改变,算法C’的次数随着n的增长,还是远小于算法D’。也就是说,与最高次项相乘的常数并不重要。
我们再来看第三个例子。算法E是2n^2+3n+1,算法F是2n^3+3n+1:
| 次数 | 算法E(2n^2+3N+1) | 算法E'(n^2) | 算法F(2n^3+3N+1) | 算法F'(n^3) |
|---|---|---|---|---|
| n = 1 | 6 | 1 | 6 | 1 |
| n = 2 | 15 | 4 | 23 | 8 |
| n = 3 | 28 | 9 | 64 | 27 |
| n = 10 | 231 | 100 | 2031 | 1000 |
| n = 100 | 20301 | 10000 | 2000301 | 1000000 |
当n=1的时候,算法E与算法F结果相同,但当n>1后,算法E的优势就要开始优于算法F,随着n的增大,差异非常明显。通过观察发现,最高次项的指数大的,函数随着n的增长,结果也会变得增长特别快。
我们来看最后一个例子。算法G是2n^2,算法H是3n+1,算法I是2n^2+ 3n+1:
| 次数 | 算法G(2n^2) | 算法H(3n+1) | 算法I(2n^2+3N+1) |
|---|---|---|---|
| n = 1 | 2 | 4 | 6 |
| n = 2 | 8 | 7 | 15 |
| n = 5 | 50 | 16 | 66 |
| n = 10 | 200 | 31 | 231 |
| n = 100 | 20000 | 301 | 20301 |
| n = 1000 | 2000000 | 3001 | 2003001 |
| n = 10000 | 200000000 | 30001 | 200030001 |
| n = 100000 | 20000000000 | 300001 | 20000300001 |
| n = 1000000 | 2000000000000 | 3000001 | 2000003000001 |
这组数据应该就看得很清楚。当n的值越来越大时,你会发现,3n+1已经没法和2n^2的结果相比较,最终几乎可以忽略不计。也就是说,随着n值变得非常大以后,算法G其实已经很趋近于算法I。于是我们可以得到这样一个结论,判断一个算法的效率时,函数中的常数和其他次要项常常可以忽略,而更应该关注主项(最高阶项)的阶数。
判断一个算法好不好,我们只通过少量的数据是不能做出准确判断的。根据刚才的几个样例,我们发现,如果我们可以对比这几个算法的关键执行次数函数的渐近增长性,基本就可以分析出:某个算法,随着n的增大,它会越来越优于另一算法,或者越来越差于另一算法。 这其实就是事前估算方法的理论依据,通过算法时间复杂度来估算算法时间效率。
8. 总结
算法的定义: 算法是解决特定问题求解步骤的描述,在计算机中为指令的有限序列,并且每条指令表示一个或多个操作。
算法的特性: 有穷性、确定性、可行性、输入、输出。
算法的设计的要求: 正确性、可读性、健壮性、高效率和低存储量需求。算法特性与算法设计容易混,需要对比记忆。
算法的度量方法: 事后统计方法(不科学、不准确)、事前分析估算方法。在讲解如何用事前分析估算方法之前,我们先给出了函数渐近增长的定义。
函数的渐近增长: 给定两个函数f(n)和g(n),如果存在一个整数N,使得对于所有的n>N,f(n)总是比g(n)大,那么,我们说f(n)的增长渐近快于g(n)。于是我们可以得出一个结论,判断一个算法好不好,我们只通过少量的数据是不能做出准确判断的,如果我们可以对比算法的关键执行次数函数的渐近增长性,基本就可以分析出:某个算法,随着n的变大,它会越来越优于另一算法,或者越来越差于另一算法。




